Reinforcement Learning (RL)

Reinforcement Learning (RL)

Reinforcement learning is inspired by the way humans and animals interact with their surroundings through interaction. In order to emulate such a situation in a binary world, an agent is defined to act as an entity (human/animal) in the digital world and interact with its defined environment.

The main goal of the agent is to learn a policy by receiving feedback from the surrounding environment. This policy serves the agent well by maximizing the agent’s long-term reward. To learn the policy, the agent constantly observes the current state of the environment, takes an action, receives feedback from the taken action, and then updates its knowledge based on the feedback.

Hence, there are the following main components in RL (Reinforcement Learning):

1. Agent: The agent is the actor in the defined environment, learning how to interact and survive/live in the environment.

2. Environment: The term speaks for itself. It is where the agent resides and interacts with its surroundings. The environment could be either virtual or physical.

3. State: The state represents the most updated situation of the agent in its environment.

4. Action: An action is the chosen decision of the agent when interacting with its environment. The agent has a set of possible actions it can take in each state to update its knowledge of the policy and transition to a new state.

5. Reward: The reward is the feedback that the agent is provided with in its environment regarding its performance of the chosen action. The agent’s goal is to maximize the cumulative reward over the long run.

Reinforcement learning finds applications in various domains such as game playing, autonomous vehicles, robotics, resource management, and recommendation systems, just to name a few.

Reinforcement Learning Projects

I have applied my knowledge in the implementation of Reinforcement Learning (RL) in the Gridworld and Pacman environments, as illustrated below.

Value Iteration

One of the algorithms used in Reinforcement Learning (RL) is value iteration. It is a dynamic programming algorithm employed to solve Markov decision processes (MDPs), which are mathematical models representing sequential decision-making problems in reinforcement learning.

An MDP is defined by a set of states, actions, transition probabilities, rewards, and a discount factor. The objective is to find an optimal policy that maximizes the expected cumulative reward over time. Value iteration is an iterative algorithm that enables the computation of the optimal value function and policy for an MDP.

Implementation of Value Iteration

Value iteration algorithm is implemented to be applied to both Gridworld and BridgeGrid worlds, as described below.

Application of Value Iteration in Gridworld

One of the environments that facilitates the understanding of concepts in Reinforcement Learning (RL) is Gridworld. In Gridworld, the environment is represented as a grid of cells, with each cell being in one of several states. Typically, the agent’s objective is to navigate through the grid to reach a specific goal state while avoiding obstacles or penalties. The agent can move in the four cardinal directions (up, down, left, right) and may encounter rewards or penalties when transitioning to a new state.

The following demonstrates the computation of optimal values and its execution for 10 iterations in Gridworld. The “values” are depicted as numbers within the squares, “Q-values” are shown as numbers within the quadrants of the squares, and “policies” are represented by arrows pointing out from each square. In each iteration, the agent starts from the initial state, takes an action to transition to a new state, and updates its policy based on the feedback received. The updated policy ultimately assists the agent in acting optimally within the environment to reach the final destination.

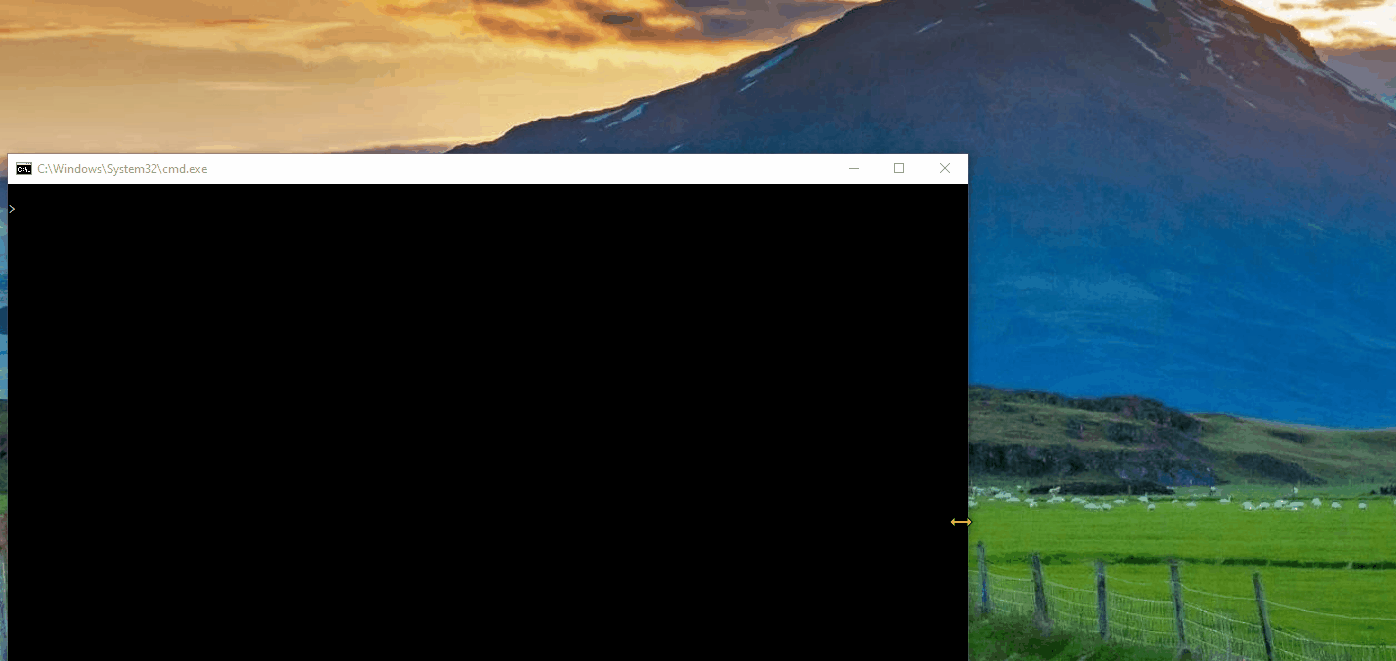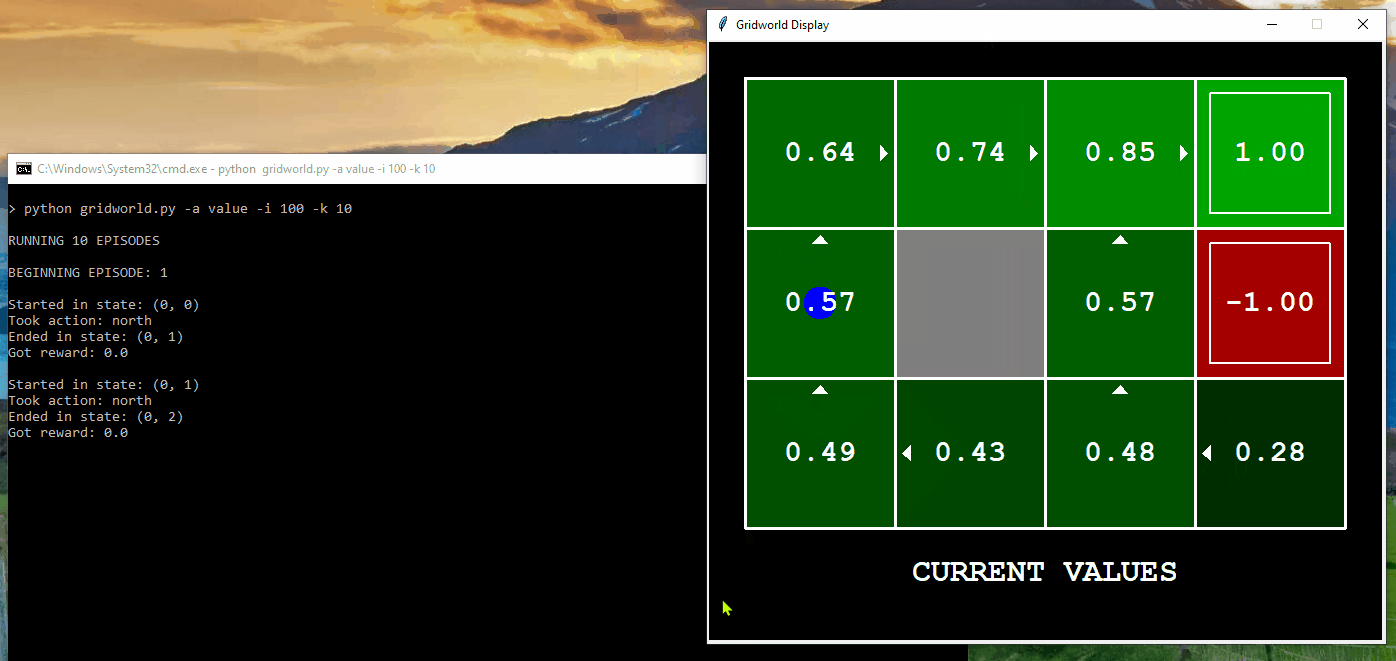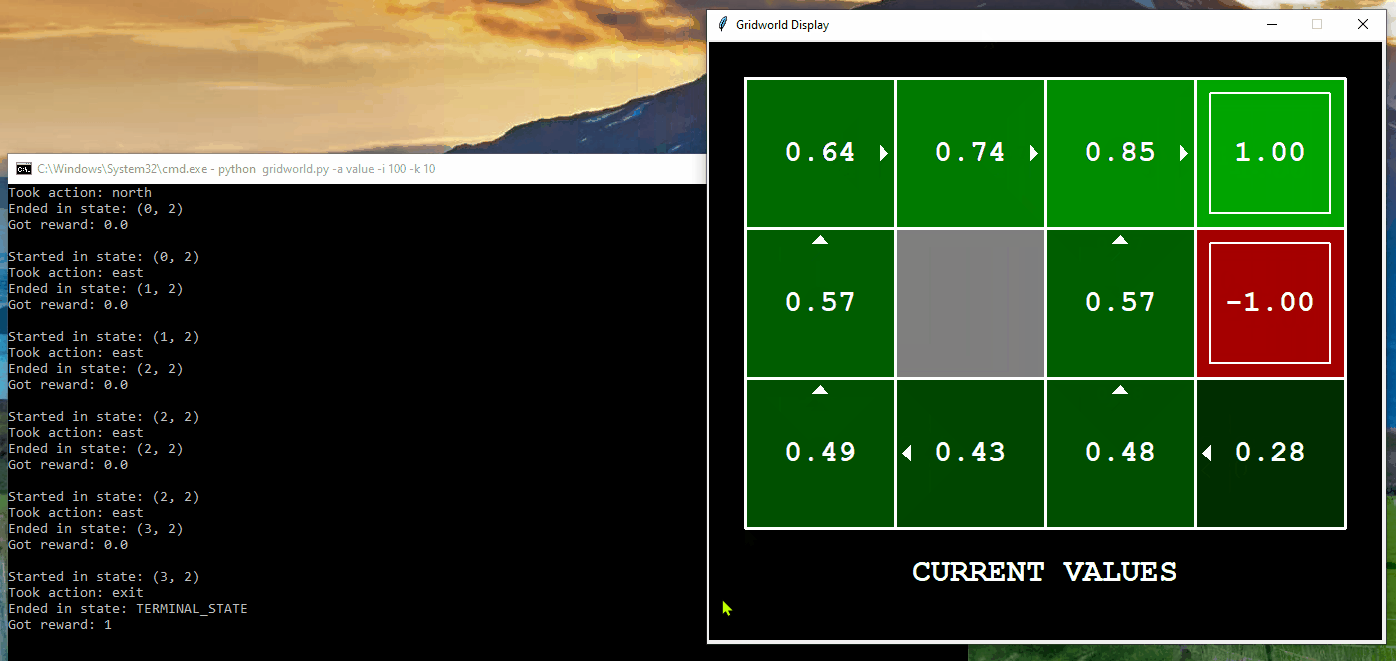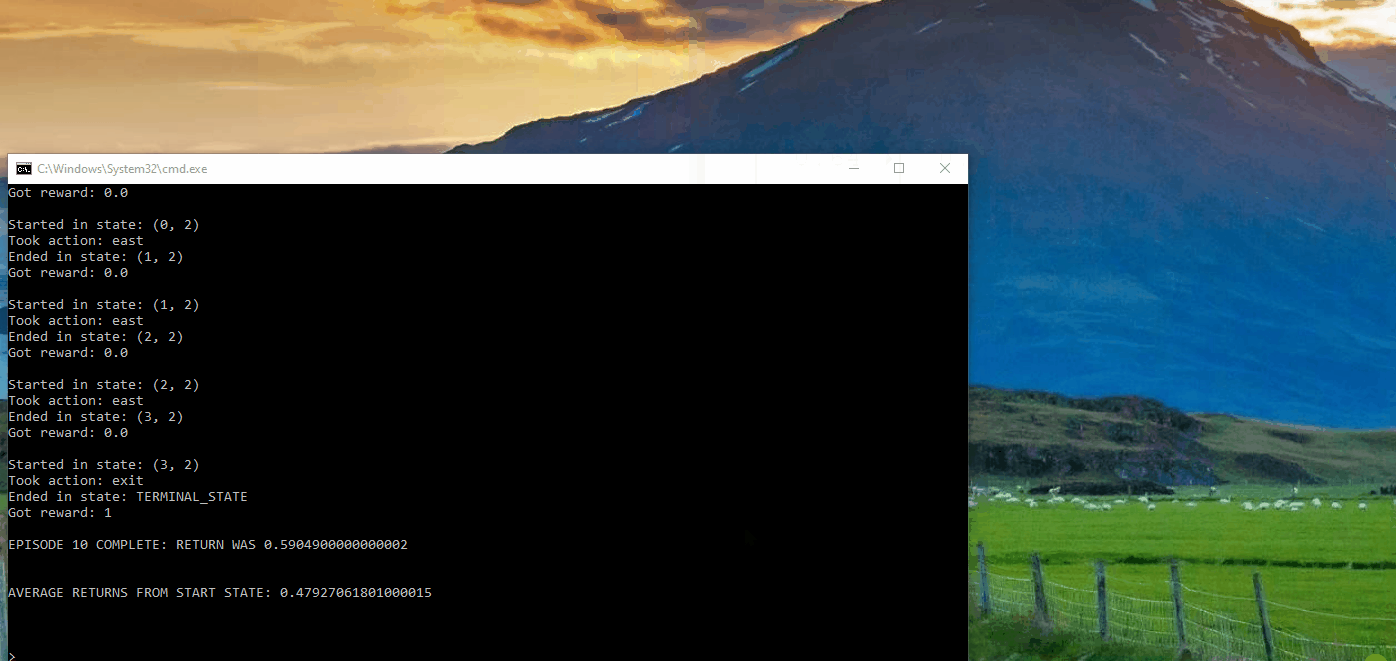
Application of Value Iteration in BridgeGrid

The following is the BridgeGrid, which consists of low- and high-reward terminal states separated by a narrow “bridge.” On either side of the bridge, there is a chasm with a high negative reward. The agent initially starts near the low-reward state and aims to reach the high-reward state. Through the process of updating its policy using value iteration, the agent can ultimately reach the final destination.

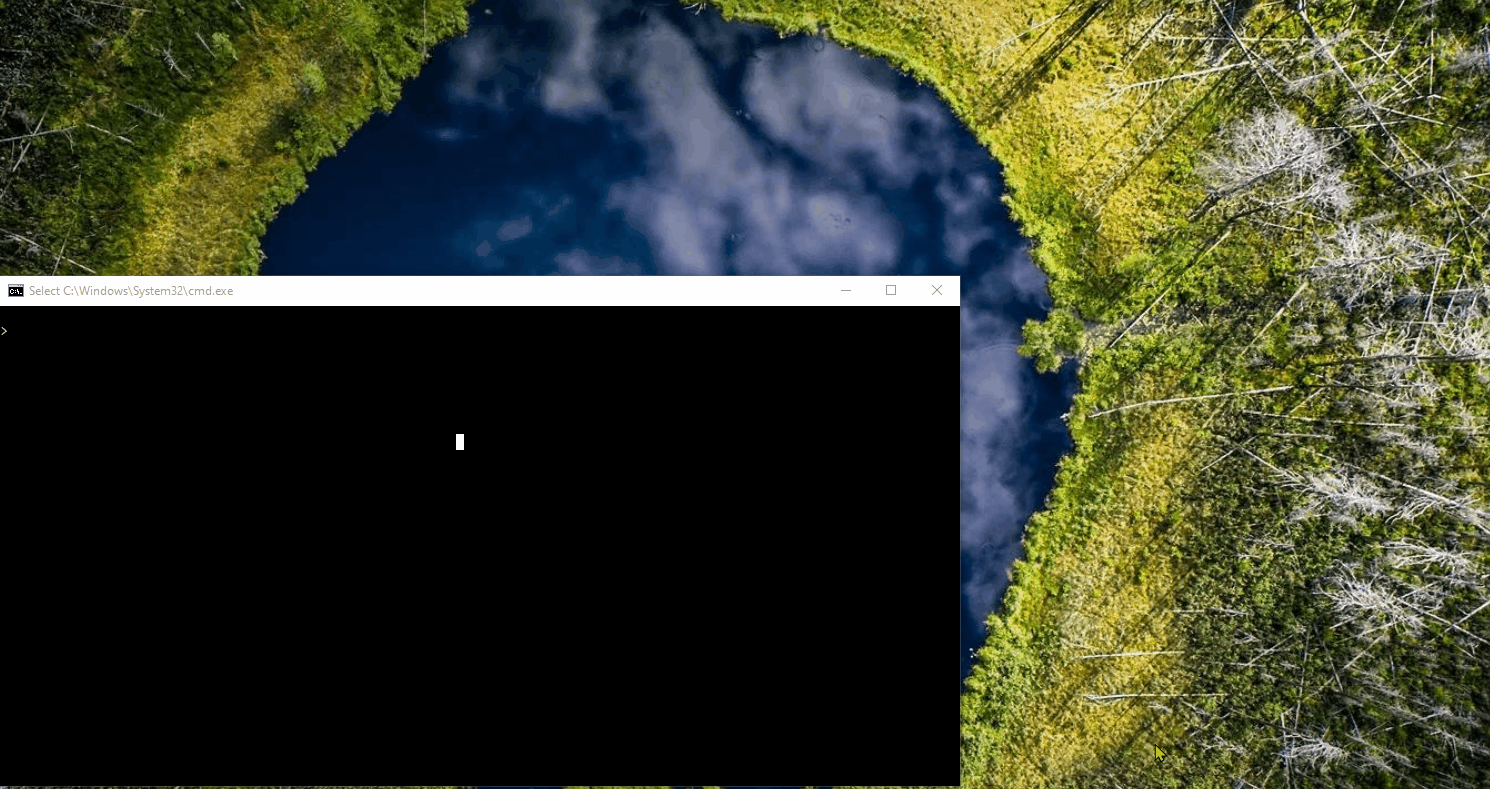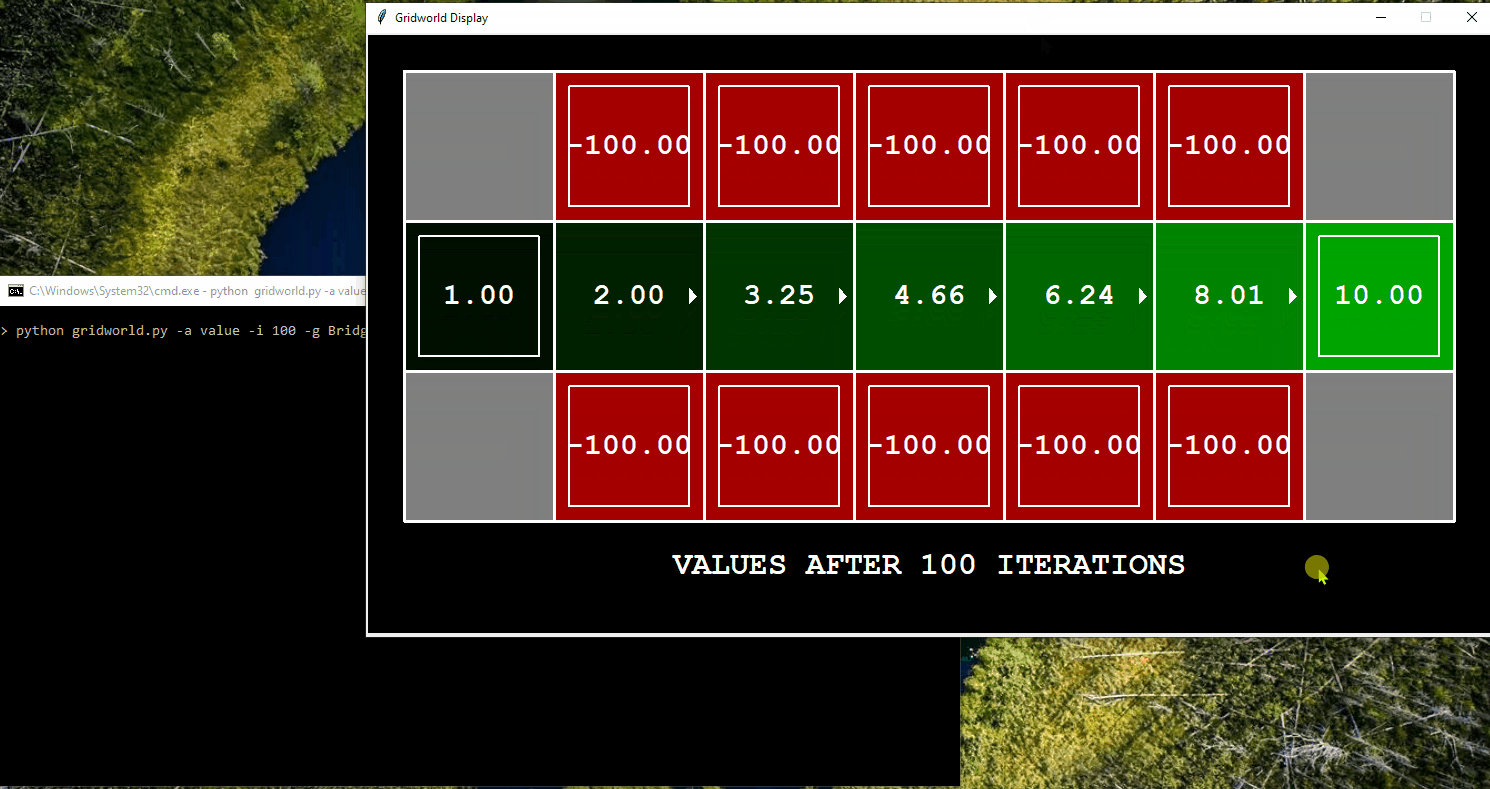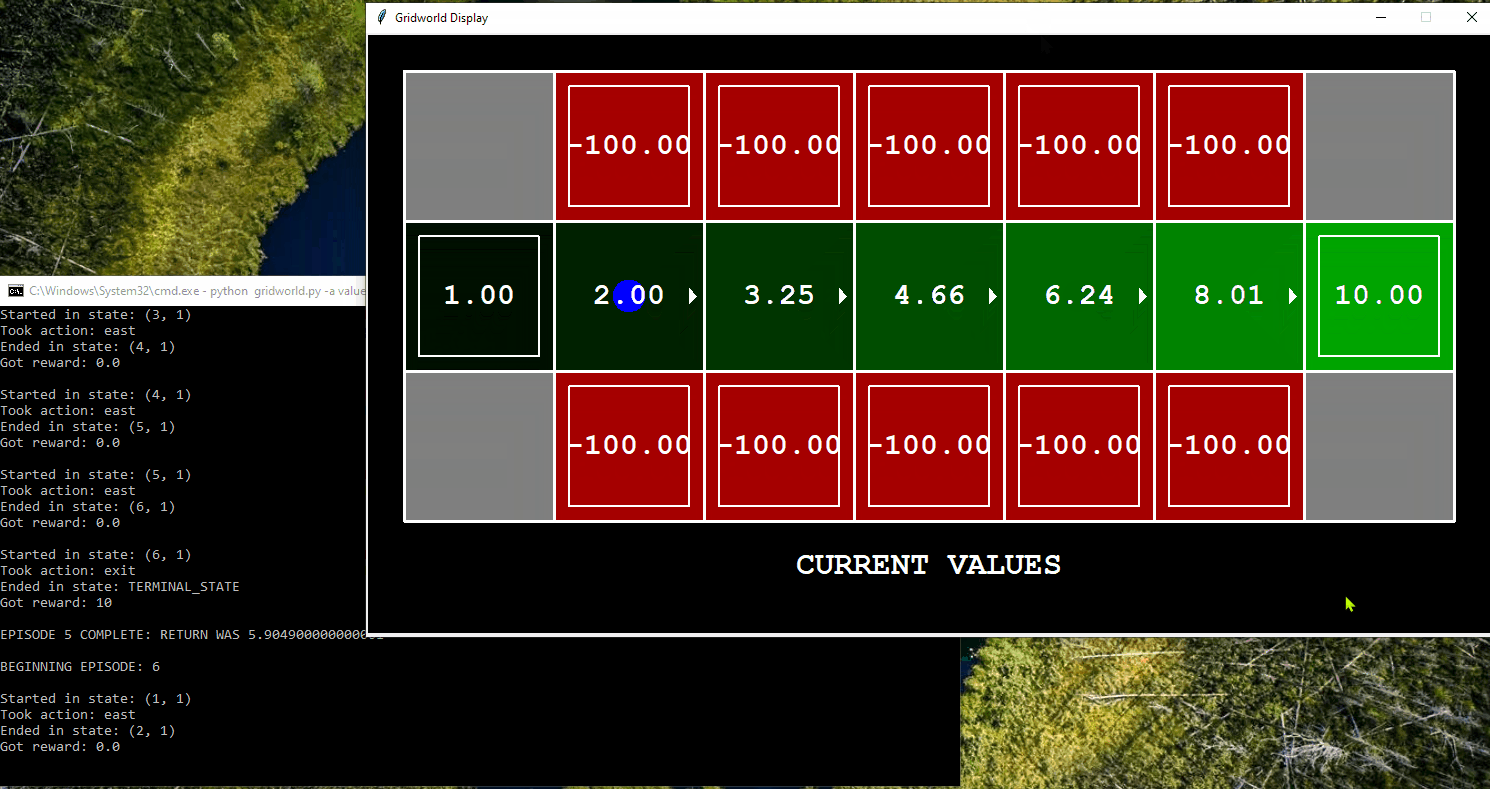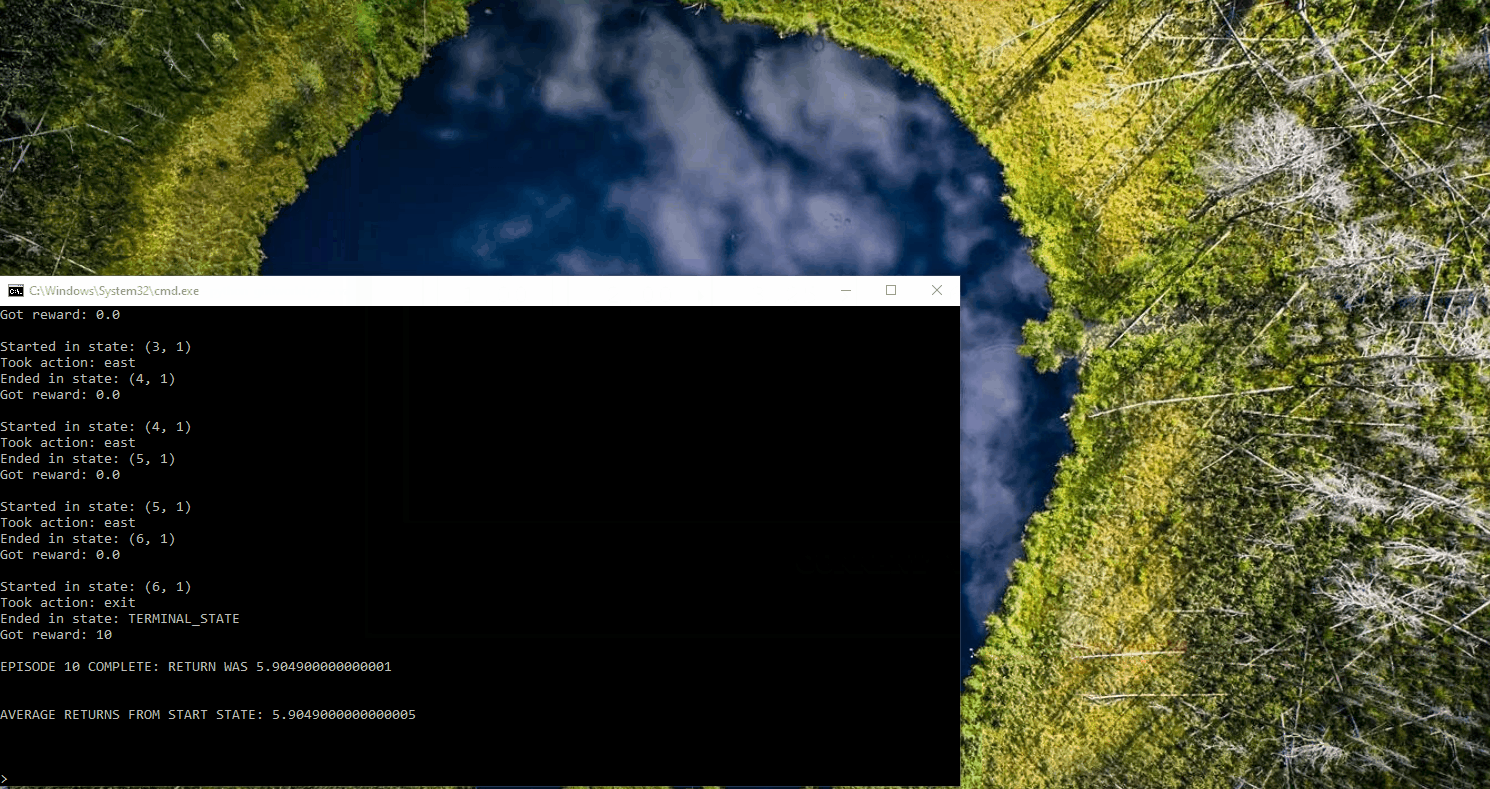
Asynchronous Value Iteration

Asynchronous Value Iteration (AVI) is a reinforcement learning algorithm utilized for solving Markov Decision Processes (MDPs). It extends the classic Value Iteration algorithm by addressing computational efficiency through asynchronous state value updates, as opposed to synchronous updates.

In the Value Iteration algorithm, all state values are simultaneously updated in each iteration. However, in AVI, the state values are updated asynchronously, meaning that only a subset of states are updated in each iteration. This approach proves advantageous in large MDPs where updating all states in every iteration would be computationally expensive.

By allowing asynchronous updates, AVI facilitates parallelization and distributed computation, making it suitable for large-scale problems where computational efficiency is crucial. However, this comes at the cost of some accuracy in state value estimation, as the updates may not consider the most recent values of all states, but it enables faster convergence.

Implementation of Asynchronous Value Iteration

The Asynchronous Value Iteration algorithm is implemented and can be applied to the Gridworld environment, as described below.

Application of Asynchronous Value Iteration in Gridworld

The following displays the final result of computing a policy using Asynchronous Value Iteration and executing it for 10 iterations with 1000 iterations each. A notable feature of this algorithm is its runtime, which is less than a second for this case, making it highly efficient.

Prioritized Sweeping Value Iteration

Prioritized Sweeping Value Iteration (PSVI) is an algorithm utilized in reinforcement learning to update state values efficiently in a Markov Decision Process (MDP). It is an extension of the classic Value Iteration algorithm that incorporates prioritization of state updates based on their potential impact on other states.

In traditional Value Iteration, all state values are updated in each iteration according to the Bellman equation. However, PSVI focuses on states that have a higher likelihood of affecting other states or possess greater potential for learning. By prioritizing the order of state updates, PSVI aims to converge more rapidly and allocate computational resources more effectively.

The prioritization of state updates in PSVI enables more efficient exploration of the state space, as it prioritizes updates for states likely to have a substantial impact on the overall value estimation. By focusing on updates based on their potential importance, PSVI can achieve faster convergence compared to traditional Value Iteration, particularly in large-scale MDPs.

Implementation of Prioritized Sweeping Value Iteration

The Prioritized Sweeping Value Iteration algorithm is implemented and can be applied to the Gridworld environment, as described below.

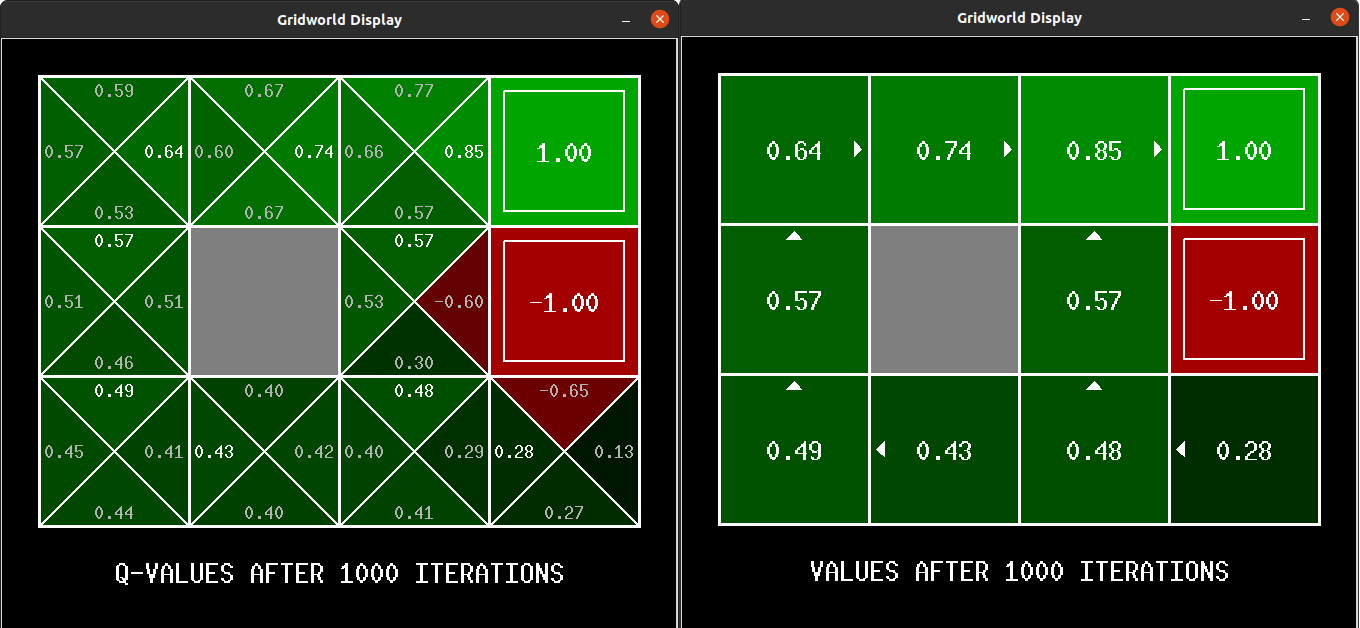
Application of Prioritized Sweeping Value Iteration in Gridworld

The following displays the final result of computing a policy using Prioritized Sweeping Value Iteration and executing it for 1000 iterations. Similar to Asynchronous Value Iteration, a key feature of this algorithm is its quick runtime, taking less than a second to execute for this case.

Q-Learning

One caveat of the value iteration algorithm is that the agent does not learn from experience. Instead, all its actions are based on the pre-computed Markov Decision Process (MDP). While this limitation may not be significant in a simulated world like Gridworld, it becomes a concern in real-world scenarios where the true MDP is unknown or inaccessible.

On the other hand, an agent equipped with the Q-Learning algorithm can learn from experience by interacting with its environment. By iteratively updating Q-values based on observed rewards and estimated future values, Q-Learning gradually learns the optimal action-values for each state. Once the Q-values have converged to their optimal values, the agent can utilize them to select the best actions in any given state and follow an optimal policy.

Implementation of Q-Learning

The agents in Gridworld and Pacman environments are going to be equipped with Q-learning in order to navigate and survive in their respective environments. A detailed description is provided below.

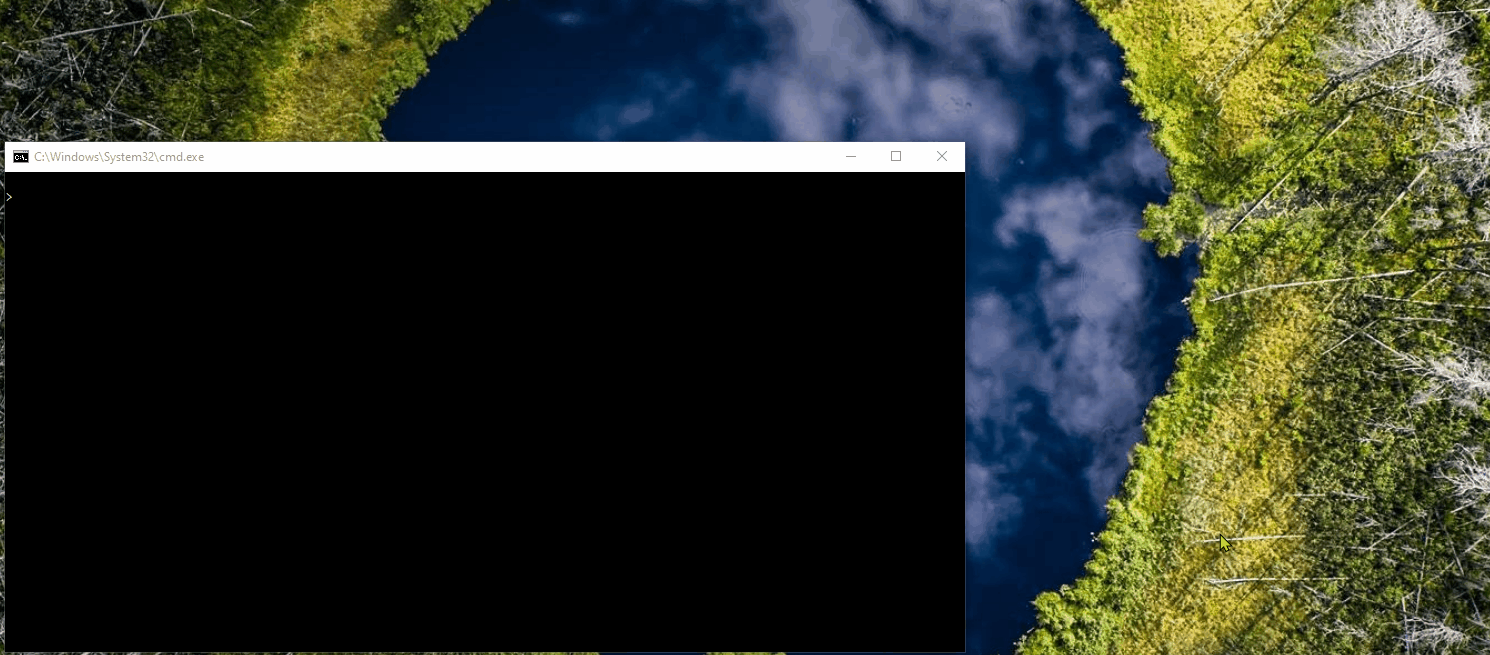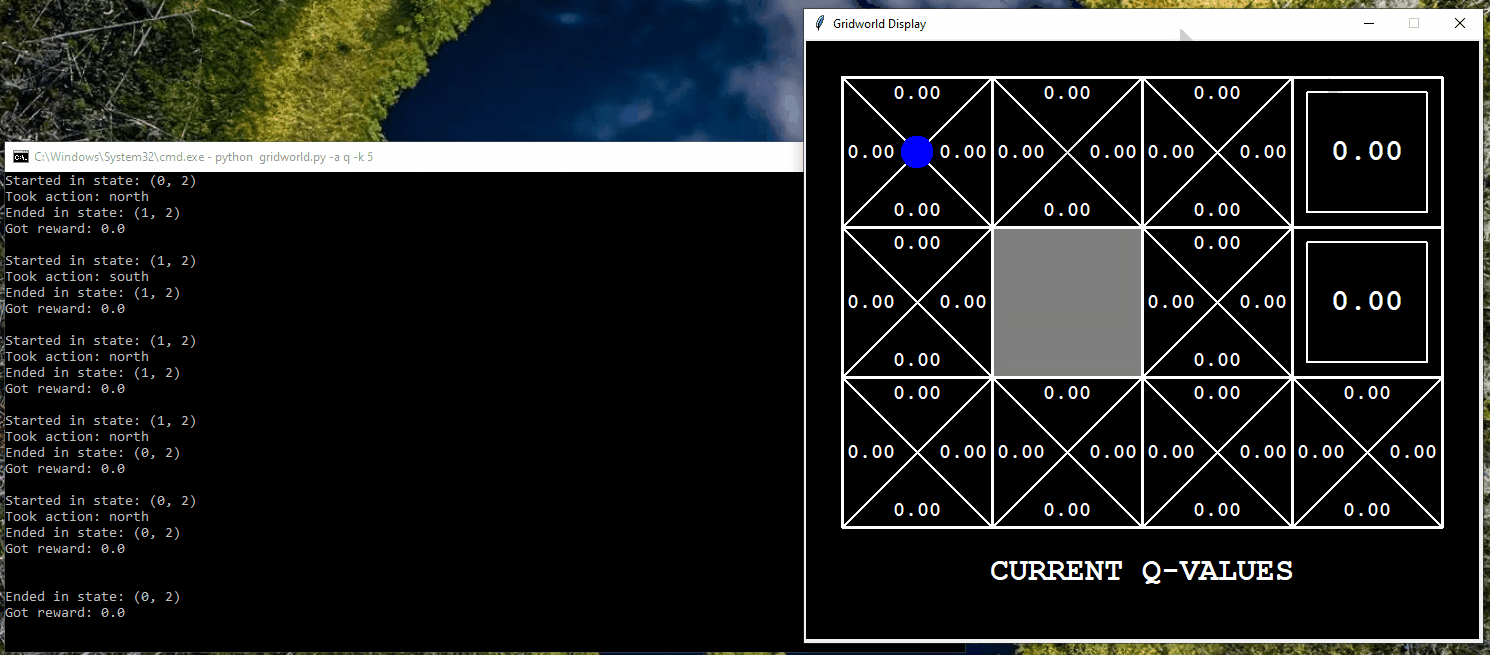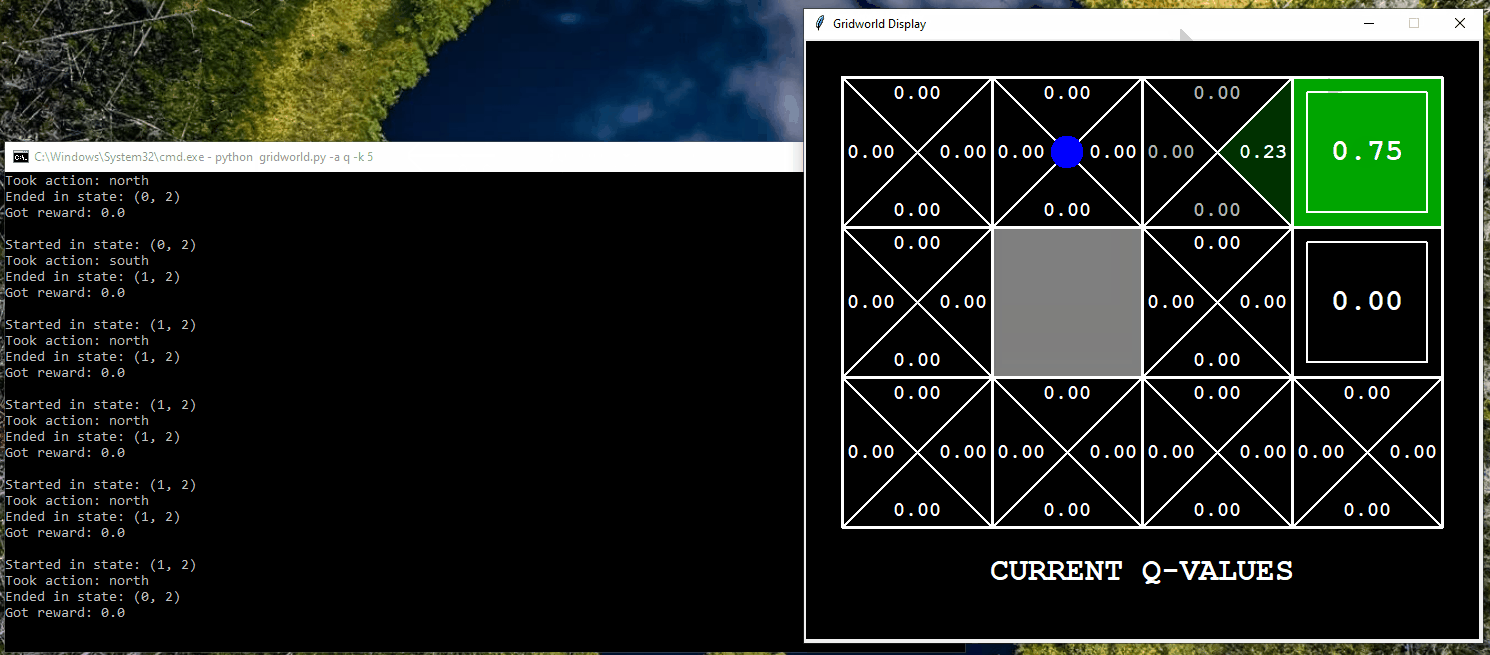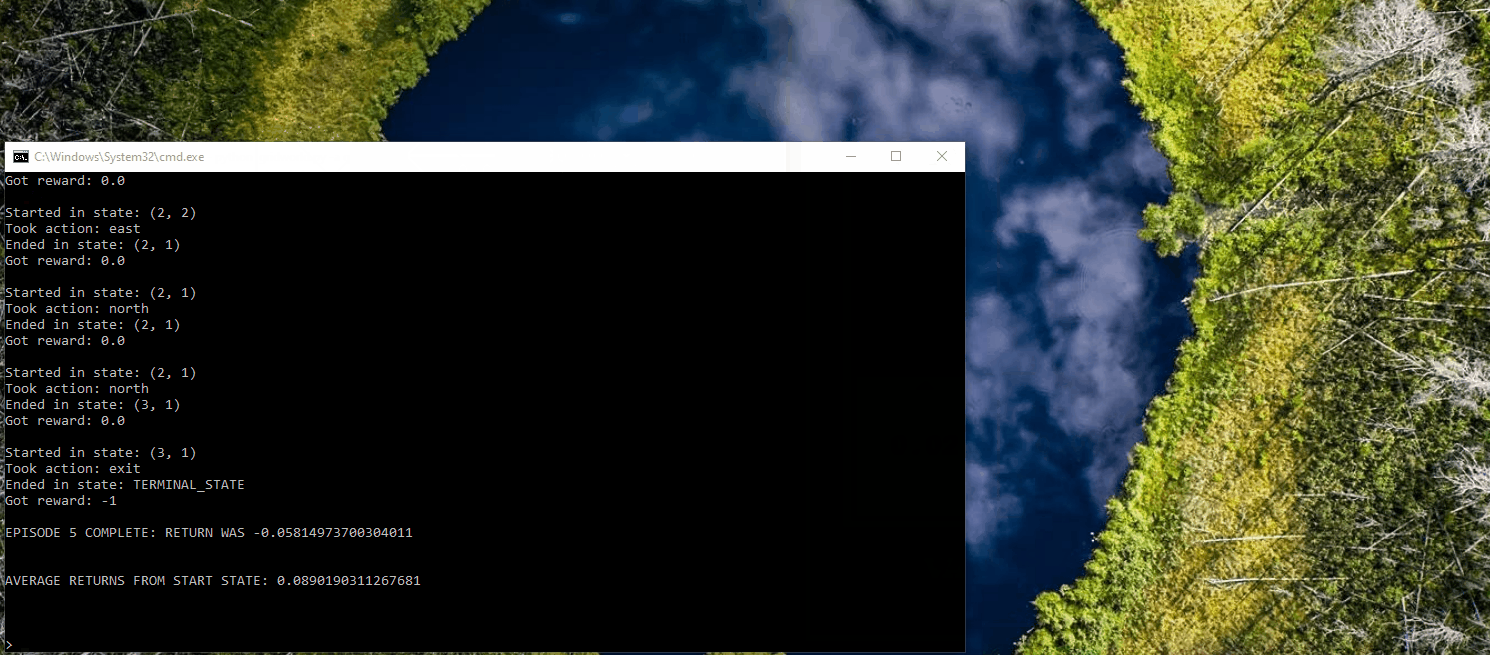
Application of Q-Learning in Gridworld

The following displays the agent, represented by a blue dot, interacting in the Gridworld environment using a trial-and-error approach to learn which actions to take in order to reach the goal. In this particular example, the agent has the opportunity to interact with the world for only five iterations.

Application of Q-Learning in Pacman

The Pacman agent aims to win the game by exploring the environment and reaching its goal. To learn the policies, Pacman plays the game a total of 2010 times. In the first 2000 rounds, no graphical user interface (GUI) is shown to expedite the learning process. However, in the last remaining 10 rounds, we can observe how Pacman has learned to play in its world during the last 10 rounds out of the total 2010 rounds.

Caveat

We saw how the Pacman has learned to play in its world. However, if we modify its environment, such as by increasing the size of the board, Pacman would need to relearn everything in the new world. It implies that Pacman lacks the ability to generalize its knowledge across different worlds. Whatever it learns in a specific world applies only to that particular world. This approach is clearly not scalable.

Implementation of Approximate Q-Learning

Q-learning encounters limitations when the environment where the agent lives becomes larger. These limitations primarily manifest in terms of memory usage and computation time. Storing and calculating Q-values for all states in a large environment becomes increasingly impractical. However, Approximate Q-learning addresses this limitation by employing function approximation techniques to predict Q-values.

Application of Approximate Q-Learning in Pacman

To expedite the policy learning process, Pacman is equipped with the Approximate Q-learning algorithm, which leverages the fact that certain states may share common features. By utilizing this algorithm, increasing the size of the environment should not be a cause for concern. The following demonstrates the implemented outcome of Approximate Q-learning.

_{Reference link}